Joel Watson

Joel.Watson92@gmail.com | LinkedIn: /in/joel3rbear | Twitter: @Joel3rBear

---

Project maintained by JoelMWatson Hosted on GitHub Pages — Theme by mattgraham

Home » Blogs » Merge Quick Walkthrough

---

Stepping Through Quick Sort

The way quick sort works is by selecting a pivot at the end of the array, then comparing each value in the array with the pivot and putting larger numbers to the right of the pivot and smaller numbers to the left. then you recursively call mergeSort on all of the left and right partitions of the array never having to compare elements from one partition with elements from another.

Using the the input array [8,4,23,42,16,15], we will be going through the pseudocode below showing the the output at each step.

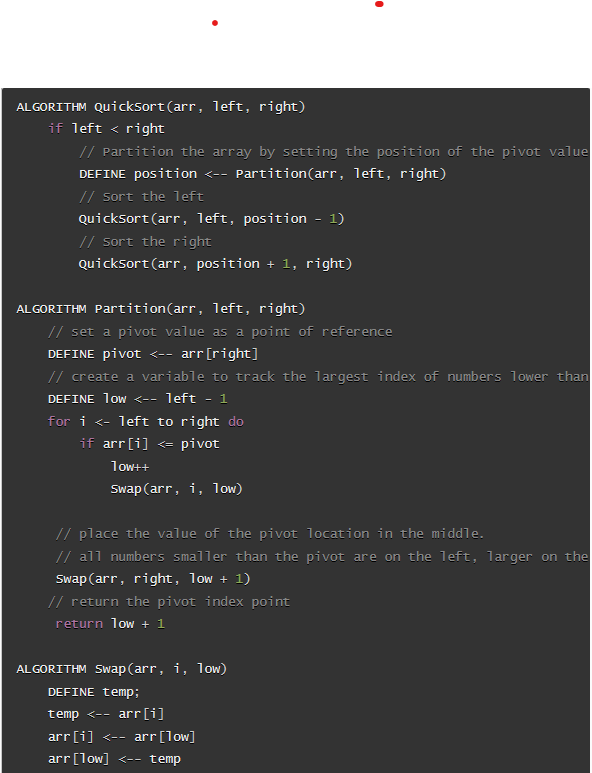
In the first step we use the last element in the array as the pivot. In this case that was the number 15. We compare 8 and 4 and find them to be smaller so we swap their positions with the lowest unsorted index and raise the unsorted index by 1 each time. In this case 8 and 4 were in the indexes 0 and 1 which were also the lowest unsorted indexes so we didnt move them at all. We then move forward with our comparisons and find the rest of the elements to be larger than the pivot. When we reach the end of the array, we swap the pivot with the lowest unsorted index.

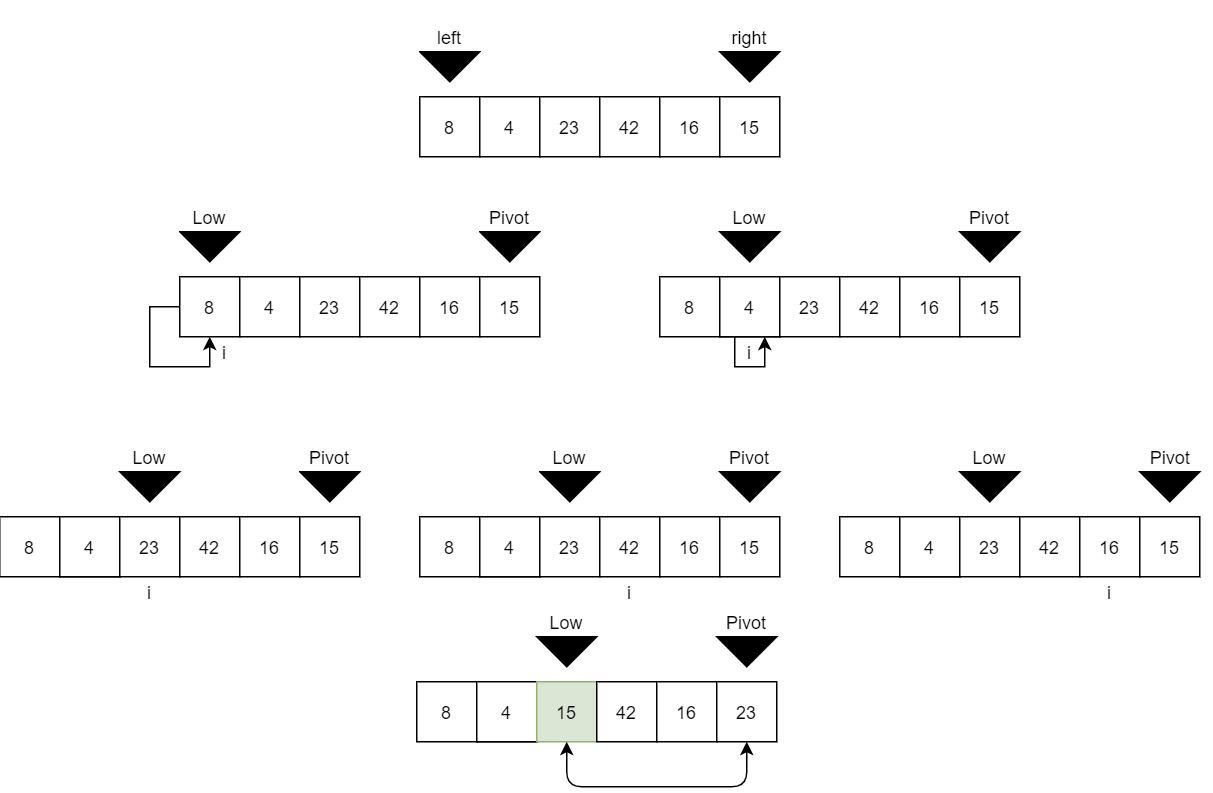
For step 2 we now how two array partitions, [8, 4] and [42, 16, 23]. We call quicksort on both arrays and go through the same process. In the first array we swap 8 and 4. In the second array since 42 is larger we move forward and compare 16 and 23. Since 16 is smaller we swap their positions with the lowest unsorted index (42) and then reach the end of the array and swap the pivot with the lowest unsorted index (42 again);

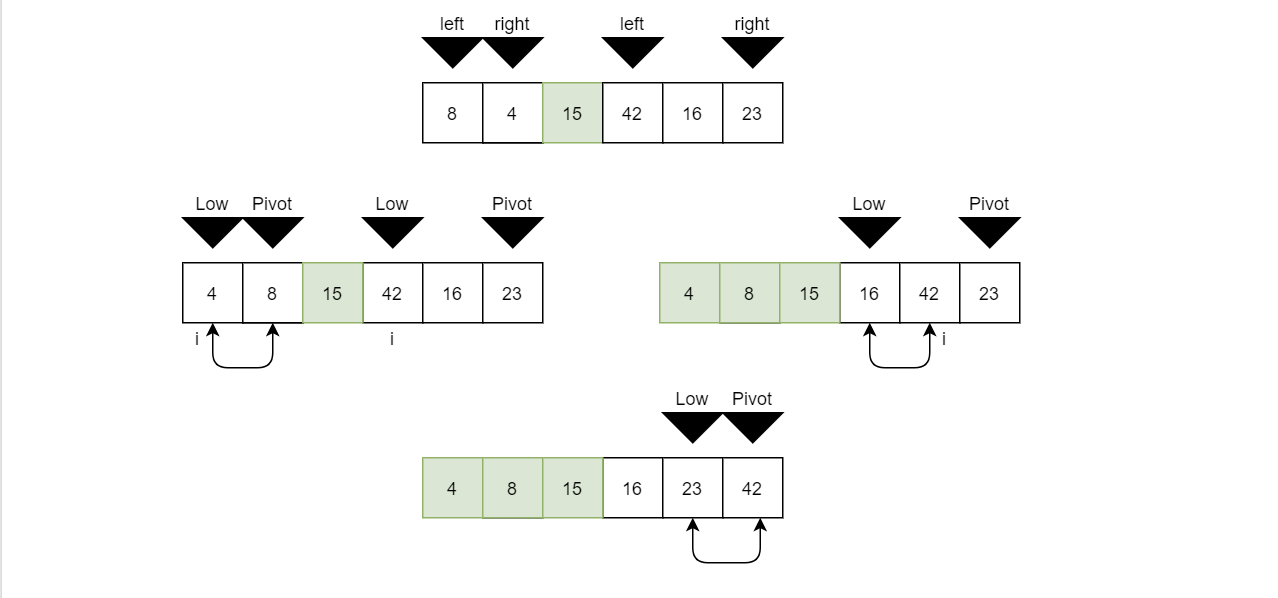
For this step we have two single element arrays left to sort, [16] and [42]. Since they are only one element long, you know they are going to be sorted correctly so you can return without swapping any positions.

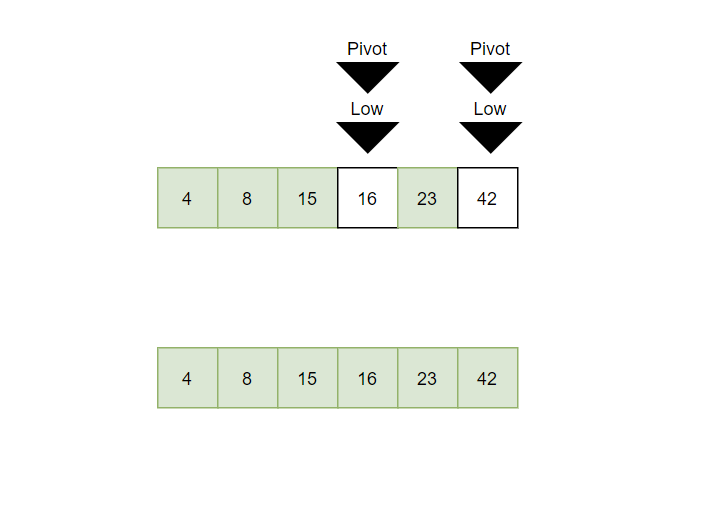
Finally can return the sorted array of [4,8,15,16,23,42].