Joel Watson
Joel.Watson92@gmail.com | LinkedIn: /in/joel3rbear | Twitter: @Joel3rBear
Project maintained by JoelMWatson Hosted on GitHub Pages — Theme by mattgraham
Home » Blogs » Merge Sort Walkthrough
Stepping Through Merge Sort
The way merge sort works sort of in two phases. In the first phase, it recursively calls itself to break the array in half until it has single element long arrays. In the second phase it then begins comparing the values at each index of the arrays and merging them back into the original array.
Using the the input array [8,4,23,42,16,15], we will be going through the pseudocode below showing the the output at each step.
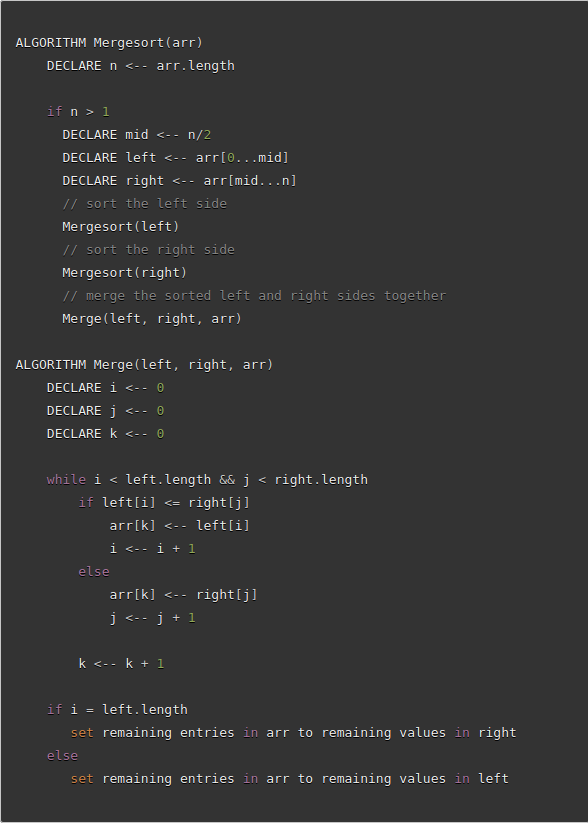
In the first step we divide the array in two and save the first half of the array as “left” and the second half of the array as “right”. We recursively call merge sort first with the “left” array and then with the “right” until we are left with arrays of length 1.
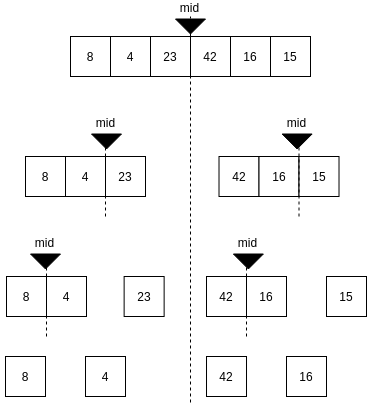
At this point we start to compare the values at each index of the array and place them back into the array they were split from in the correct order. In this case we start by comparing [4] with [8], and placing the two single element arrays back into a 2 element array with [4,8]. We also compare [42] with [16] and move them back into 2 element array with [16,42].
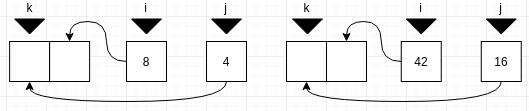
In this step, we have a 2 element and a 1 element array that we need to compare. First we compare the front element of each array, which ever array has the smaller value at this position moves its value into the original array and the counters for this array and the original array are incremented. In our case, on the left side we have to compare [4,8] and [23], and on the right we have [16,42] and [15]. These merge into [4,8,23] and [15,16,42].

Now we are down to the final two arrays to merge, [4,8,23] abd [15,16,42]. We merge these in the same process as the above step, starting at the head of the array and moving down. Once you reach the end of one array, the left over elements from the other array are added to the original order.
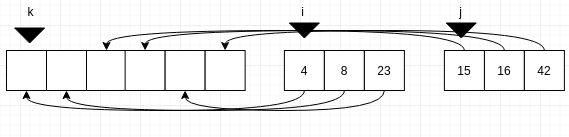
Finally can return the sorted array of [4,8,15,16,23,42].
